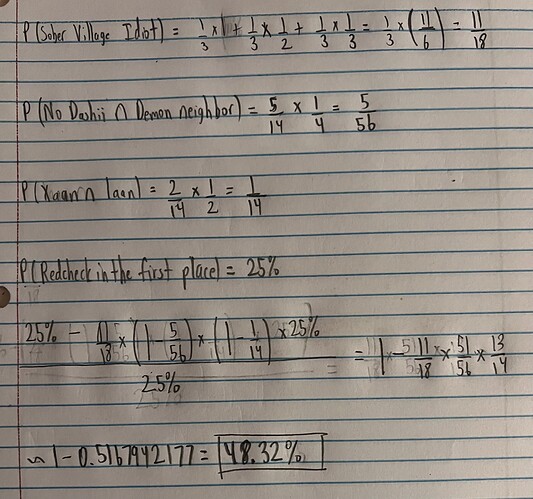3 minutes…
Public statement from the executives and shareholders of Chomp’s:
We blundered and will keep a more positive eye on the hydra
carbonated has nominated Ash.
damn. sleepy.
sword nimi remains impatient
perhaps tomorrow will bring things into more light
So the way I’m approaching this is:
Major Assumption
Socially, I believe that the host is always going to give you a good check on D1 if they can because the lack of information we have outside of that means we always act on a redcheck minus insane socials, especially given that you were targeting a slot who will inevitably have an enormous impact upon the game (spent far too much time trying to find the Madoka Magica term for this). This is a major assumption, but I believe in it strong enough to run with it.
I’m also assuming you’re town and not made mad by a Cerenovus, but that feels like less of a jump.
Probability Calculation
We are calculating the probability you got a bluecheck given that BetterMittens is a redcheck. The formula for conditional probability is P(A and B) / P(B).
In this case, A is the scenario where you get a bluecheck, and B is the scenario where BetterMittens is mafia.
P(B) is easy: assuming you’re town, BetterMittens has a 2/8 = 25% chance of being a Minion or Demon.
P(A and B) - the probability you both get a bluecheck and where BetterMittens is mafia - is harder, but we can simplify it. There are four possibilities:
- Bluecheck + Town
- Redcheck + Town
- Bluecheck + Mafia ← What we’re solving for
- Redcheck + Mafia
Because of our major assumption, we strike out #2.
Additionally, we assume that for #1, the Storytellers would leave your check untainted. Thus, it equals the base probability that BetterMittens is town: 6/8 = 75%.
We know that the probability of all four options will add to 100%. We have that the probability of Option 1 is 75% and that the probability of Option 2 is 0%. Therefore, the probabilities of Option 3 and 4 add to 25%.
In a more intuitive sense, this mirrors the base probabilities of being town and mafia: we’re looking at subsections of those probabilities.
So our goal is simple: find the probability that your redcheck could not be messed with in any way (as per our major assumption, if your redcheck could be messed with, the Storytellers would mess with it), subtract that from 25%, then divide that by 25% to get our final probability.
More Assumptions, Weeeeeee
This is the part where we need to make some giant assumptions. That said, if you disagree with the numbers I use, you’re free to change them accordingly.
- Equal probability of being a sober Village Idiot:
- 1 Village Idiot - Guaranteed to be sober
- 2 Village Idiots - 1/2 chance to be sober
- 3 Village Idiots - 1/3 chance to be sober
- Equal probability of which Demon and Minion is in play, removing Kazali-Xaan (1/14 for each pairing)
- Equal probability of Demon location (1/4 chance for the Demon to be your neighbor)
- The Xaan: By far my biggest leap, but I imagine the GMs will lean towards having a different number of Outsiders if they added this in. Given that 9 of us gives 2 Outsiders, I suspect they will either lean towards 1 Outsider or 3 Outsiders. I’m guessing the probability distribution would look like 50%-20%-30% because I do not think the Storytellers would add 4+ Outsiders to a game this small.
- 1 Outsider: 50% chance
- More than 1 Outsiders: 50% chance
Everything else should be accounted for: Boffin can’t trigger unless you are literally the Demon (see Major Assumption), and Sweetheart only triggers on death.
The Actual Math
Result
Given our numerous assumptions, there is a 48.32% chance that BetterMittens is mafia given that you got a bluecheck.
Time to finally backread.
Numbers have been sent.
As you well know, being wrong is very quick.
TL;DR
There is literally a Result section at the bottom.
Okay but 2/3 chance to be sober for 3 village idiots and also are you saying the fact that we got checked increases our odds to be mafia?
Your math is wrong
Litten that broke the whisper
–May
Jarek broke the whisper
2/3 odds to be sober from base, yes.
But I think I have screwed up my probabilities, now that you mention it.
The probability you calculated cannot be the probability we are mafia as otherwise being a red check would have to inverse the probability right?
Ok, I think I calculated the probability Chomps gets a bluecheck assuming you’re mafia rather than the probability you’re mafia assuming Chomps gets a bluecheck.
And that literally doesn’t make sense how being checked raises hour chance of being mafia to 50/50
P(B|A) instead of P(A|B), so to speak.