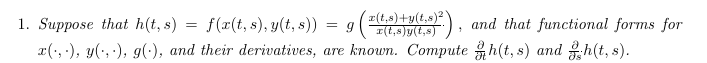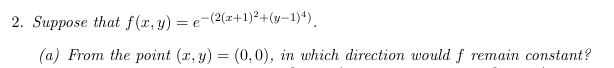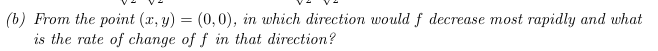oh
that’s less bad than I thought
I… can see a way where you compute every partial derivative of order 6 or less manually, and that prooooooooobably works (assuming my thought on how to do multivariable taylor series is correct)
that is probably a Bad way to do it though
That’s a lot of fucking partials
yeah the only way it’d be reasonable is if everything cancelled really nicely
which… it might do, based on some thoughts and wolfram’s answer
I just lied and said all of them have a sin(~) in them so they’re all zero
Because I didnt want to do the problem
I need to talk to those guys I know in the class so I can have wise advisors on my side
the first partial (of any variable) should be 0 because the cos(stuff) becomes -sin(stuff) * stuff’, and stuff(0, 0, 0) = 0
this should also work for the third and fifth partials
I think this is plausible but I didn’t know it was true so by my principles it’s a lie
Second-order derivatives also all have a sin(~) in them
For the record the other problems on this thing are like
LITERALLY FINE it’s just this one that’s decided to fuck with you for no reason and make you hell calculate a ubnch of numbers because you go “surely this is also easy”
i know what functional forms means :) (lying)
Ever heard of the saying “form over function”? Ever heard of “centrism”?
I don’t know either but I’m just assuming “x(., .) has a known functional form” means “you can write x(., .) = some function of the inputs”
If we were explicitly told what a functional form was I didn’t remember it but I made this same assumption
it’s been a while since i’ve done calc 3 idr how to do that problem. i assume the partial derivatives end up being nice somehow
theres three of them??
ohhh. those functional forms. like. “we know what x, y, and g are in forms of functions”
