atp we have to make atleast 1 assumption
More than willing to say that Badeline is mafia over LittleLee.
Keep in mind that Goose has been advocating your township all game, and actively defending your slot from being wagoned, whilst also taking a far more neutral approach to Lee. This was a neutral stance you took of each other. It’s “easy” because it looks correct, not because we’re lazy. If you’re town, you have to shine like a star.
With that said… yeah, probably, Kanave.
this sucks
it’s like this game was engineered in a lab to be the ideal game for scum
well fuck
i wrote a theory post for you guys last night
so i’m gonna post it
this might be some of the highest stakes solving I’ve ever done
Day 4 Game Theory Dot Post
As usual, this post does not account for social solving, only pure mathematics.
Vocabary
Within this post I will be describing players the following way:
Group 1 are Lee and Badeline (that are in a 50/50 together)
Group 2 are the 6 remaining players.
The cleared townies are LT1-3
Anonygoose is W1
Group 1 consists of W2 and 1T
Group 2 consists of W3 and 2T1-5
In addition, I will be using standard notation for probabilities, as follows:
P(X) is the probability of X happening
P(X’) is the probability of X NOT happening
P(X∩Y) is the probability of X AND Y happening
P(XΔY) is the probability of X OR Y happening
P(X∪Y) is the probabiliy of AT LEAST ONE of X or Y happening
Approach 1: Raw Dogging 3/3
In this method, we combine W1 with one of Group 2 and one of Group 3 (fig i)
P(A) is a 3/3 result
P(B) is a 2/3 result
P(C) is a 1/3 result
The two scenarios of P(B) (That is, P(W1+W2+2T1-5) and P(W2+2T+W3) ) are indistinguishable (fig. iii) which means that we gain less (although not no) information from it, although P(AΔC) are ideal.
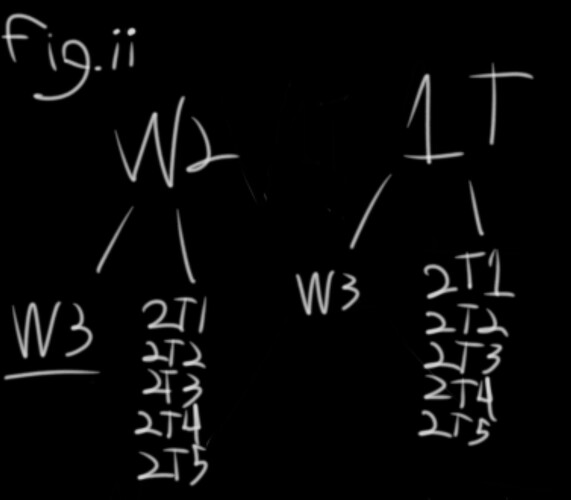
P(A) = P(W2∩W3) which has a 1/12 chance (fig. ii)
P(B) = P(W2ΔW3), which means there is a 6/12 chance, although the two outcomes are not equally likely: A 5/6 chance that this result contains W2 and a 1/6 chance that this result contains W3 (fig. iii)
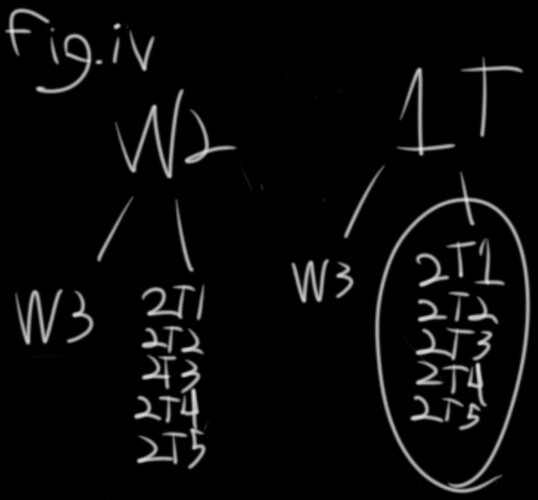
P(C) = P((W2∪W3)’), which means there is a 5/12 chance (fig. iv) to have a second wolf locked and a third inside of 1/5
There’s a clear method for solving P(B) if we really must, so all three of these options are beneficial.
Because choosing to switch means you are independently taking the initial odds again, counterintuitively you have a better chance of switching into w2 than w3- even though w2 is more likely to happen the first time, it’s also more likely to happen the second time as well.
Approach 2: Cross Examining Groups 1 and 2
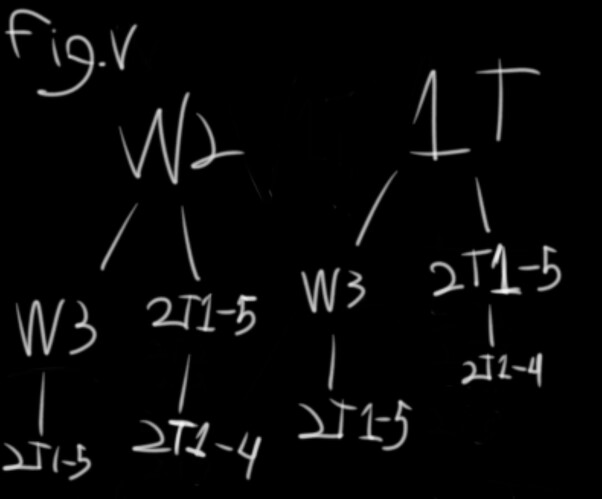
This method disregards W1 entirely, attempting to solve W2 and W3 by checking one within G1 and two within G2. (fig. v)
P(D) is a 2/3 result
P(E) is a 1/3 result
P(F) is a 0/3 result
As per usual, we aim for P(D) or P(F), as the middle result is the worst. The results of P(E) are indistinguishable from each other, and although they are not equal, we don’t have the luxury of solving it in the same way as P(B). P(F) implies W2 and reduces W3 to 1/4, while P(D) wins us the game outright tomorrow.
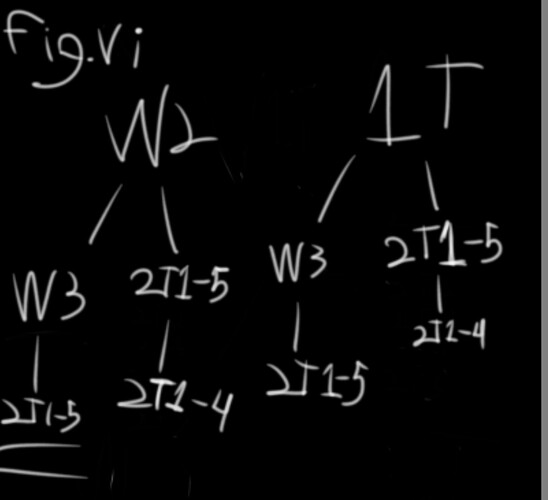
P(D) = P(W2∩W3), which is 5/50 (fig. vi)
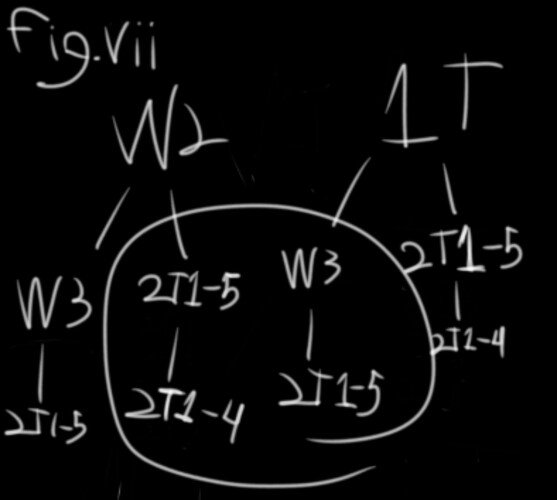
P(E) = P(W2ΔW3), which is 25/50 (fig. vii)
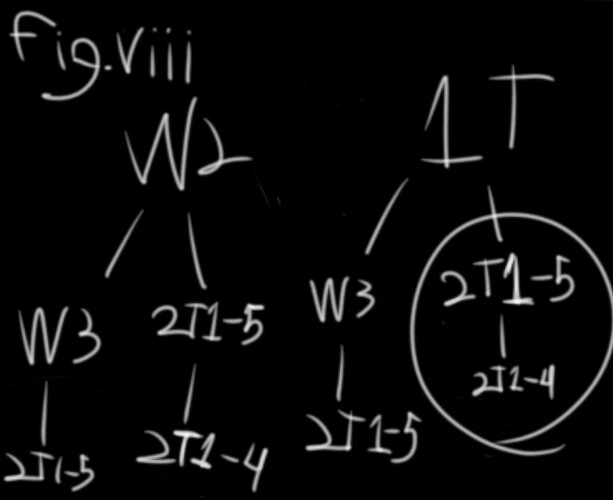
P(F) = P((W2∪W3)’), which is 20/50 (fig. viii)
In my opinion, this is the worst of our options because it does not let us win tonight and the undesirable result is worse going into the next day.
Option 3: Combing the Final 6
This method is the same as option 3 from yesterday, although with one wolf down, it may be worth it.
P(G) is a 1/3 result
P(H) is a 0/3 result
P(GΔH) = 10/10 chance to give us a 1/6 chance of solving tomorrow. If there are any masons in the final 6, this can vary drastically- but only upwards.
Option 4: Using LT1 to Comb the final 6
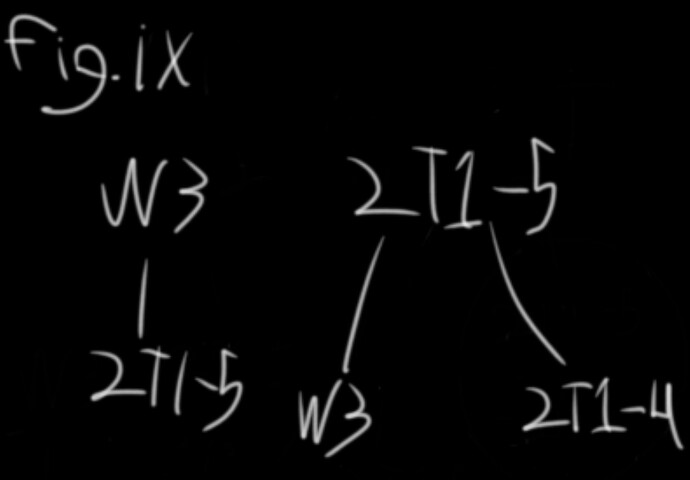
This method uses a known slot to implement a slightly more risky version of Option 3. (fig. ix)
Using LT1 or No Prisoner 1 means that:
P(I) is a 1/3 result
P(J) is a 0/3 result
You could also use W1 instead, in which case:
P(I) is a 2/3 result
P(J) is a 1/3 result
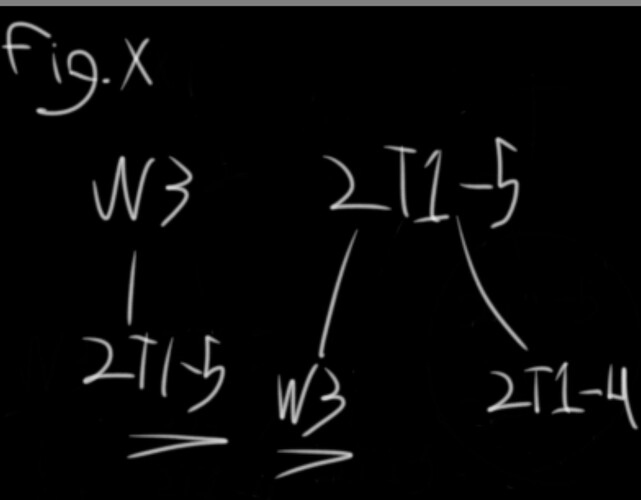
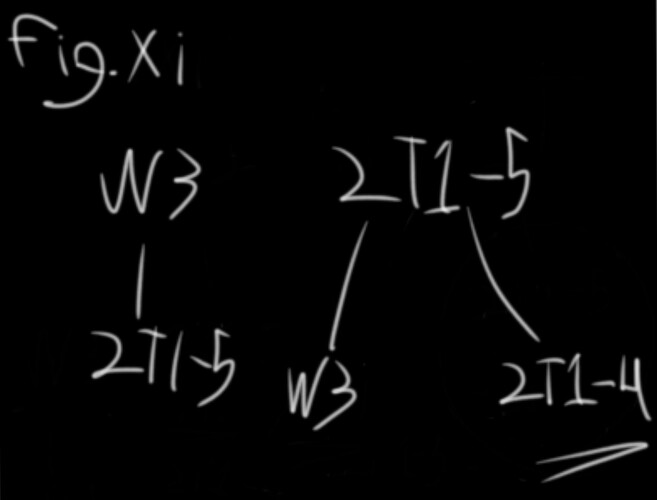
P(I) = P(W3), which has a 10/30 chance to reduce W3 down to 1/2 (fig. x)
P(J) = P(W3’), which has a 20/30 chance to reduce W3 to 1/4 (fig xi)
Analysis/D5 Game Theory
This whole post is moot if Mafia guessed all three masons N3.
P(AΔD) are guaranteed victories, so the rest of this part does not matter.
P(B) and P(E) can both be solved via the Monty Hall Problem, with a 1/2 chance that switching works. If we choose not to switch, though, it’s because of social reads- That’s entirely possible and also correct. P(E), however, requires at least an extra day to confirm results. It’s too slow.
P(C) is a less guaranteed victory, although a 1/5 chance is not bad considering the gamestate
P(F) catches W2 and isolates W3 to 1/4, meaning it’s slightly better - but much riskier, considering P(E)- than simply avoiding this method
P(GΔH) is a guaranteed chance to isolate the final wolves to 6 possible combinations. The only probability in Method 3 comes with potentially catching Masons inside of P(G), which can, theoretically, raise the 1/6 to a 1/4 or even 1/2 with some extreme luck- it requires that we have not jailed 1-2 masons up to this point and that we DO jail those 1-2 today alongside the wolf.
P(I) is a straightforward 1/3 chance to reduce the combinations to 4, but the failstate (P(J) is a 2/3 chance to reduce the combinations to 8, among the lowest of the remaining methods. This is also modified by Masons in the same way as P(G) and P(H).
It should be noted that 1T could also theoretically be a mason. If they out themselves as mason, W2 is outed, so double the chances of hitting the maximum possible wolves in any method involving checking Group 1.
TL;DR
Method 1 is the safest, with even the worst result being a cliche’d probability problem.
Method 2 is the worst, with about half chance to have us spinning our wheels.
Method 3 has become a high-risk high-reward strategy where our results can vary wildly based on how many masons are left and whether or not they claim.
Method 4 is even higher risk for an even higher reward strategy than Method 3, but with a 2/3 chance to be in the worst spot of any of these methods.
In my opinion, Method 1 is probably the best for the current stage of the game: A 1/10 chance to win instantly, a 1/12 chance of winning mathematically the next day, and a 2/5 chance to be only slightly worse than some slightly more risky options. The last 5/12 combos would be rough under a mathematical framework, except that if we aren’t Switching in our Monty Hall Problem it’s because we decided that Doors 1 and 2 were linked in some way, so we know which ones are misses (or, in our case, hits)
this post is made to be valuable for any town allignment and future proofed for the next time this setup is in this situation
I’d rather not just “accept a loss” when we have more than enough time to actually reevaluate everything, which I’ve basically been begging people to do for a full day straight.
but it’s useless right now
anyway luckily for us no masons have been checked
Through sheer diligence and wagon control.
Not Voting (12): Quail, Chomps, LittleLee, Ash, Anonygoose, Kanave, Magnus, spookycat27, pandora, RedPandas, FusionMoon314, Badeline
I’m probably gonna put my head down and try to case lee, my reads have obviously been off all game so I’m not comfortable trying to pursue anything outside of what I know for a fact.
That’s fair, I’m not just going to hard lock you 100% scum but I’ll definitely need a convincing arguement
I appreciate that. At the very least it won’t be coming anytime soon, probably later tonight if I have time.